Cross-validation is a widely used technique in machine learning and data science to evaluate the performance of predictive models. It involves partitioning a dataset into training and validation sets and then using the validation set to estimate the model’s prediction error. One of the most common types of cross-validation is k-fold cross-validation, which involves dividing the data into k subsets and using each subset as a validation set in turn. Another popular method is leave-one-out cross-validation, where each observation is used as a validation set once, and the remaining data is used for training.
In this article, we will explore the differences between k-fold cross validation vs leave one out cross-validation and when to use each method.
K-fold Cross-validation
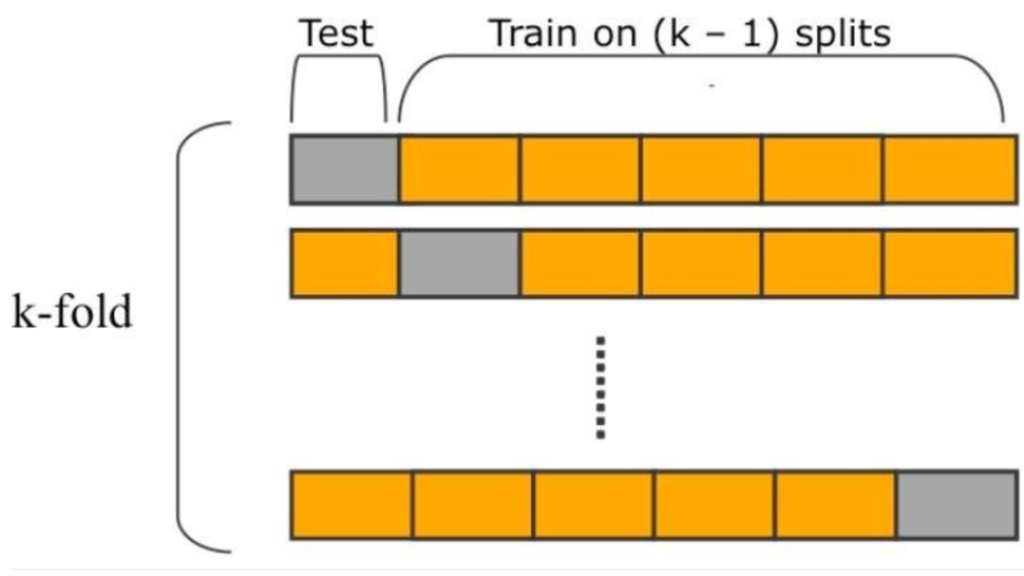
K-fold cross-validation is a popular method for estimating the prediction error of a model. It involves dividing the data into k subsets, or folds, of approximately equal size. The model is then trained on k-1 folds and tested on the remaining fold. This process is repeated k times, with each fold serving as the validation set once. The results are then averaged to obtain an estimate of the model’s prediction error.
One of the advantages of k-fold cross-validation is that it provides a more accurate estimate of the prediction error than other methods, such as holdout validation, which involves randomly dividing the data into training and validation sets. K-fold cross-validation also allows for a more efficient use of data, as each observation is used for both training and validation.
However, k-fold cross-validation can be computationally expensive, especially for large datasets or complex models. The choice of k can also affect the estimate of the prediction error, with larger values of k resulting in a lower bias but higher variance.
Leave-One-Out Cross-Validation
Leave-one-out cross-validation is a special case of k-fold cross-validation, where k is equal to the number of observations in the dataset. In this method, each observation is used as a validation set once, and the remaining data is used for training. This process is repeated n times, where n is the number of observations in the dataset.
One of the advantages of leave-one-out cross-validation is that it provides an unbiased estimate of the prediction error, as each observation is used exactly once for validation. This method is also less computationally expensive than k-fold cross-validation, as it only requires training n models.
However, leave-one-out cross-validation can have a high variance, as the training sets are almost identical for each model. This can lead to overfitting, where the model performs well on the training data but poorly on new data. Leave-one-out cross-validation can also be sensitive to outliers, as removing a single observation can have a large impact on the model’s performance.
Accelerate Your Career in AI with Best Machine Learning Courses
When to use K-fold Cross Validation vs Leave one out
The choice between k-fold cross-validation and leave-one-out cross-validation depends on several factors, including the size of the dataset, the complexity of the model, and the desired level of accuracy. In general, k-fold cross-validation is preferred for larger datasets, as it provides more efficient use of data and is less sensitive to outliers. It is also useful for models with a large number of parameters, as it can help identify the optimal values for these parameters.
Leave-one-out cross-validation, on the other hand, is preferred for smaller datasets, as it provides an unbiased estimate of the prediction error and is less computationally expensive. It is also useful for models with a small number of parameters, as it can help identify the optimal values for these parameters.
Real-world Applications Cross-validation
Cross-validation is a widely used technique in machine learning and data science, with applications in a variety of fields, including healthcare, finance, and marketing.
- One example of its use is in the development of predictive models for cancer diagnosis. Researchers have used k-fold cross-validation to evaluate the performance of machine learning algorithms in predicting the risk of breast cancer recurrence.
- Another example is in the development of credit risk models for banks and financial institutions. K-fold cross-validation has been used to evaluate the performance of these models in predicting the likelihood of default.
Accelerate Your Career in AI with Best Machine Learning Courses
Conclusion
k-fold cross-validation and leave-one-out cross-validation are two popular methods for estimating the prediction error of a model. K-fold cross-validation is preferred for larger datasets and models with a large number of parameters, while leave-one-out cross-validation is preferred for smaller datasets and models with a small number of parameters. Both methods have their advantages and disadvantages, and the choice between them depends on several factors, including the size of the dataset, the complexity of the model, and the desired level of accuracy. By using cross-validation, data scientists and machine learning practitioners can develop more accurate and reliable predictive models, and avoid overfitting and underfitting.